Hedge Fund Crowding & The Prisoner’s Dilemma

You and a member of your gang are caught and imprisoned for your crimes. Luckily, the prosecutors don’t have enough evidence to convict you on the main charge, but they plan to get you on a lesser offense. That’s the postulate of Prisoner’s Dilemma, a specific case of game theory demonstrating how two rational individuals may act against their best interests.

The prosecutors offer you a bargain if you betray your partner. They want you to confess the crime, implicating your partner. They make the same offer to your partner. The key here is that you’re kept in solitary, and there’s no way for the two of you to communicate.

‍

The offer is this:

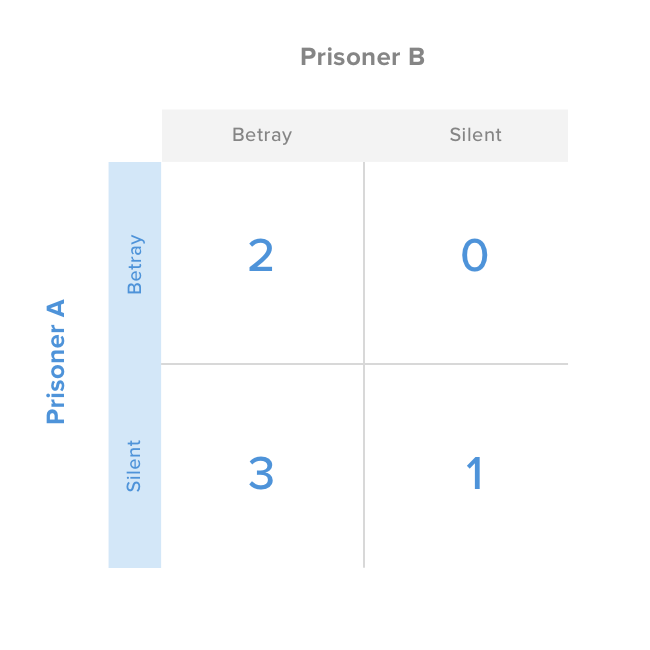
If you betray your partner and he betrays you, you both get two years in prison.

If you betray him and he stays silent, you are free to go, while he will get three years (and vice-versa).

If you both remain silent, you each get one year.

‍

Here’s what the payoff matrix for prisoner A looks like:

‍

‍

For B, the matrix is a mirror image, so combining the two looks like this:

‍

‍

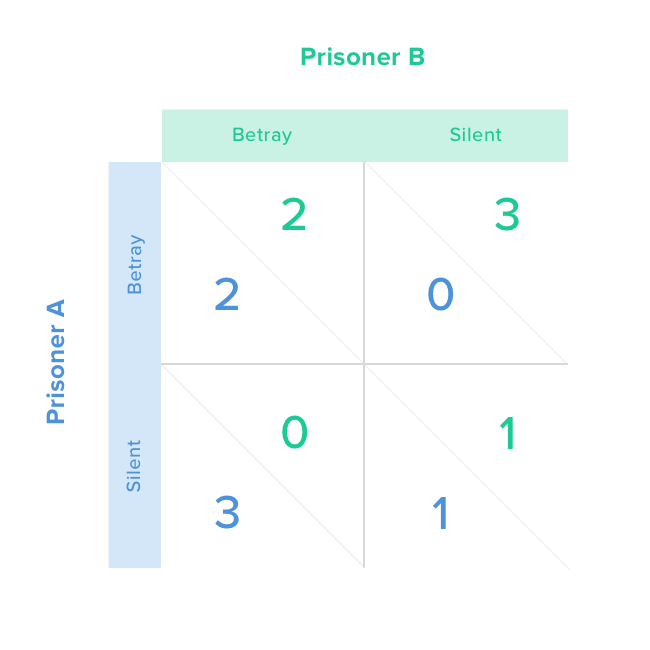
Being a rational person, you try to predict the actions of your partner. Your thinking is as follows. Let’s say he confesses and betrays you. In that scenario, it’s best to confess – you will get two years vs. three. If your partner stays silent, again it’s best to confess – you will go free vs. getting one year if you confess as well. In both scenarios, it’s best for you to betray your partner.

Yet, it’s in the prisoners’ best interest to remain silent and serve only one year. Betraying each other means serving two years. But because you don’t know your partner’s actions, you betray him to avoid the lengthy prison term and for the chance to go free.

This illustrates that in some cases, even when acting rationally, individuals don’t choose actions leading to the most optimal outcome.

This premise is a good model for hedge fund managers stuck in a crowded trade. Consider, for example, the real-life case of Valeant Pharmaceuticals (VRX) and assume there were two large hedge funds in the trade, both sizable enough to cause significant downward pressure if they sold. On October 21, a negative report came out, and VRX shares plunged 20% that same day. Let’s say the two managers can either sell fully or hold, and if one of the hedge funds liquidated their position, the stock would drop another 10%. (Obviously, this is a hypothetical example with simplistic assumptions.) To make things worse, they both think it’s likely that the bad news will send the stock another 15% lower, independent of their actions.

Here is the payout matrix for the pair of hedge funds:

‍

‍

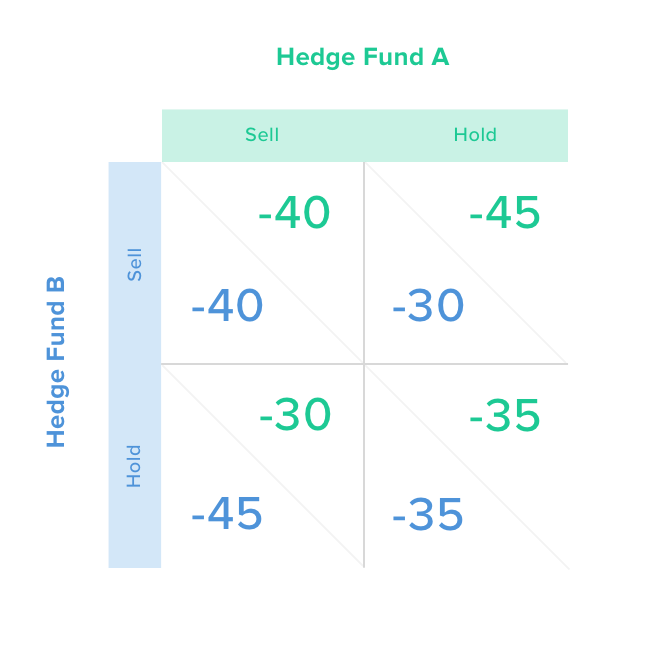
In a similar fashion, hedge funds acting rationally would both sell even though holding the stock would yield a lower loss for both of them and a better outcome. Even if they were right about the impending bad news, holding for both would lose only 35%. But if they both sell at the same time, they lose 40% (20% original drop plus 20% selling pressure—10% per each manager).

Looking at it from Manager A’s perspective, if he sells, he’ll realize a 20% initial loss plus a 10% penalty for selling his large stake quickly. But if A holds and B sells, A is stuck with a 45% loss. That’s 20% initial drop, plus 10% of manager B’s selling pressure, plus the 15% subsequent down move on bad news. Like in the original example, if manager A is trying to predict B’s action considering the price drop, the rational thing to do in both scenarios (B holds or B sells) is to sell. This explains how manager psychology exacerbates bad news in a crowded security.

‍

Why don’t the managers simply call each other and agree to hold? They aren’t precluded from conversation, like the prisoners in the original theory.

It turns out that the hold/hold state of prisoner’s dilemma is unstable. Even if the managers (or prisoners) collude, there’s overwhelming pressure to betray the other party—or sell, in the case of the managers. Knowing the other party’s reaction will give you a certain outcome, and humans are very loss averse. Furthermore, there’s always a shadow of a doubt that the other party will still betray you and act in their own self-interest despite your pact, sticking you with the worst outcome. The incentives to betray are too great.

The sell/sell state, however, is extremely stable. It’s so stable they call it the Nash Equilibrium. It’s the best outcome from each party’s perspective, though not the best outcome possible.

Having hundreds of managers in the same security adds to the complexity here, but the psychology remains the same if managers can influence price. That’s why liquidity is a key measure in our crowdedness metric for gauging this risk in all securities. Given that there are more hedge funds than stocks, it’s a situation that will likely arise more and more often. For investors who’d like to predict their hedge fund managers’ behavior, there’s never been a better time to learn some game theory.